Miscellaneous Question 43
- $A B C$ is an equilateral triangle inscribed in a circle with centre $O$.
Quantity I : Value of OD
Quantity II : Value of BD
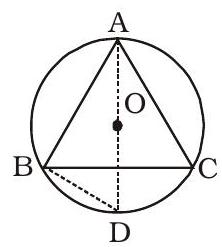
(1) Quantity I $>$ Quantity II (2) Quantity I < Quantity II
(3) Quantity I $\leq$ Quantity II
(4) Quantity I $\geq$ Quantity II
(5) Quantity I = Quantity II or No relation.
Show Answer
Correct Answer: 43. (5)
Solution:
- (5)
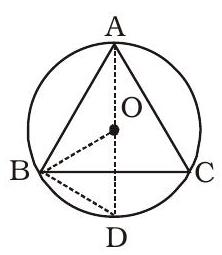
$\angle \mathrm{ABD}=90^{\circ}[\because \mathrm{AD}$ is diameter $]$
$\angle \mathrm{BDA}=\angle \mathrm{BCA}=60^{\circ}$
[Angle subtented by same arc]
$\therefore$ In $\triangle \mathrm{BOD}$,
$\angle \mathrm{OBD}=\angle \mathrm{ODB}=60^{\circ}$
$[\because \mathrm{OB}=\mathrm{OD}]$
$=\angle \mathrm{BOD}=60^{\circ}$ $\Rightarrow \triangle \mathrm{BOD}$ is equilateral.
$\therefore \mathrm{OD}=\mathrm{BD}$.
Aliter :
Diameter $\mathrm{AD}$ will bisect $\angle \mathrm{BAC} \Rightarrow$ $\angle \mathrm{BAD}=30^{\circ}$
In $\triangle \mathrm{BAD}$,
$\angle \mathrm{ABD}=90^{\circ}$
$\angle \mathrm{BAD}=30^{\circ}$
$[\because$ AD is diameter]
$\Rightarrow \angle \mathrm{BDA}=60^{\circ}$
$\Rightarrow \mathrm{BD}=\frac{1}{2} \mathrm{AD}=\mathrm{OD}$.



