Mensuration Ques 39
Question
A solid sphere of radius ’ $a$ ’ is cut by a plane at a distance of ’ $b$ ’ from its centre, thus obtaining two different pieces. The cumulative surface area of these two pieces is $40 \%$ more than that of the surface area of the sphere. Find ’ $b$ ‘.
(1) $\frac{a}{\sqrt{2}}$
(3) $\frac{a}{\sqrt{3}}$
(3) $\frac{a}{\sqrt{5}}$
(4) $\frac{a}{\sqrt{6}}$
(5) None of these
(IBPS RRBs Officer CWE (Prelim Exam) 04.08.2019)
Show Answer
Correct Answer: 3
Solution: (iii)
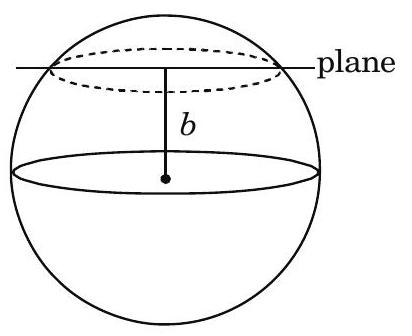
Total surface area of both pieces $=\frac{140}{100} \times 4 \pi a^{2}$ $=5.6 \pi a^{2}$ sq. units
Excess area $=1.6 \pi a^{2}$
Two extra circles are formed.
Area of each circle $=\frac{1.6 \pi a^{2}}{2}=0.8 \pi a^{2}$
$\therefore \pi r^{2}=0.8 \pi a^{2}$
$\Rightarrow r^{2}=0.8 a^{2}$
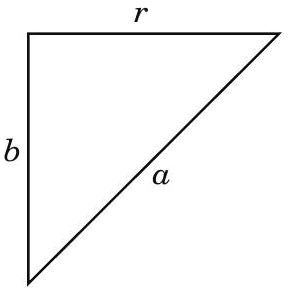
$\therefore b^{2}+r^{2}=a^{2}$
$\Rightarrow b^{2}=a^{2}-0.8 a^{2}=0.2 a^{2}$ $=\frac{2}{10} a^{2}$
$\Rightarrow b^{2}=\frac{a^{2}}{5} \Rightarrow b=\frac{a}{\sqrt{5}}$



