Mensuration Ques 29
Question
In the figure given below, $O$ is the centre of the circle. $\triangle AOB$ is an equilateral triangle while $\triangle ACB$ is isosceles with $AC=BC$. OP is drawn perpendicular to $AC$.
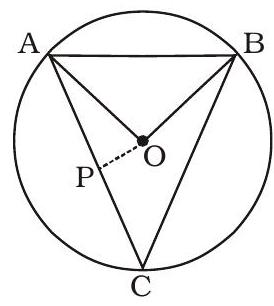
Quantity I : $\angle AOP$
Quantity II : $\angle BAP$
(1) $ I > II $
(2) $ I < II $
(3) $ I = II $
(4) $ 1 \leq II $
(5) Relationship can’t be established
(IBPS Bank PO/MT CWE (Main) 18.11.2016)
Show Answer
Correct Answer: (3)
Solution: (3)
$\angle AOB=60^{\circ}[\because \Delta$ is equilateral]
$\angle ACB=30^{\circ}[\angle AOB$ is central angle for $\angle ACB$ ]
In isosceles $\triangle$ ACB,
$AC=BC$
$\Rightarrow \quad \angle BAC=\angle ABC$ $=\frac{1}{2}\left(180^{\circ}-30^{\circ}\right)=75^{\circ}$
$\therefore \quad \angle BAP=75^{\circ}$
$\therefore \quad \angle OAP=\angle BAP-\angle BAO$ $=75^{\circ}-60^{\circ}=15^{\circ}$
Now, in right angled AOP,
$\angle AOP=180^{\circ}-\left(90^{\circ}+15^{\circ}\right)$ $=75^{\circ}$
From (i) and (ii) we have
$\angle AOP=\angle BAP$ i.e, $I=II$



